计算创意学系列(一):概念空间探索的比喻
本章考察概念空间探索的理论。这个理论最初是在认知科学学者玛格丽特·安·博登(Margaret Ann Boden)的著作《创造力心智(The Creative Mind: Myths and mechanisms)》中被正式提出,后来又在AI学者G A. Wiggins的论文《描述、分析和比较创造力系统的框架(A Framework for Description, Analysis and Comparison of Creative Systems)》中,从数学和形式理论的角度得到了更严谨的重构。
创造力(Creativity),是一个非常抽象的概念。维基百科上对这个词条的总结性解释是:
“Creativity is a phenomenon whereby something somehow new and somehow valuable is formed. The created item maybe intangible (such as an idea, a scientific theory, a musical composition, or a joke) or a physical object (such as an invention, a printed literary work, or a painting).”
“创造力是指某个具有价值的新事物被构造出来的现象。这个被创造出来的事物可以是无物理形体的 (比如一个点子,一个科学理论,一首曲子,或一个玩笑),也可以是物理对象(比如一个发明,一个印刷出来的文字作品,或者一幅画)。”
从这个定义中就可以看出,人们对于有价值的新事物被创造出来这个现象背后的机理是不清楚的,或者至少还没有达成共识。但他们假定(或者相信),一切这一类的现象,尽管有着成千上万种不同表现形式,背后有一个共同的机理。于是人们发明出“创造力(Creativity)”这个词,用以意指这些现象背后那个共同的机理。而对于这个背后的机理究竟是怎样的研究,就被称作是对创造力的研究。
对于人类创造出新事物这个现象的关注,在历史上很早就开始了,主要集中在对艺术创作领域的研究。不过在文艺复兴以前,人们并不把创造新事物的能力看作是源于人自身的。柏拉图曾提出艺术摹仿理论,认为艺术创作的本质是对感官事物的临摹,因此并不是一种真正的创作。而在希腊神话中,又设置了主司艺术和科学的缪斯女神,为创作者们带来灵感——也就是说,创作的源动力是外在于人的,而不是人自身具有的一种能力。类似的理论还有佛教中的顿悟和基督教中的天启。

源于文艺复兴运动的人文主义,开始宣扬创造新事物的能力不是来自任何神圣领域,而就是人自身具有的一种能力。到十九世纪,人们终于开始严肃地探讨创造力现象背后的机理,并且是从人自身之中寻求这种机理的解释。自此,大量关于创造力的理论,从哲学、社会学、心理学、认知科学、神经科学、艺术、经济学、语言学等等等等各种各样的学术视角被提出。
比如说,1926年由英国社会学家Graham Wallas在论文《思考的艺术(The Art of Thought)》中提到的孵化理论(Incubation Theory),建立了包含四个过程:1)准备(积累相关知识和技能) 2)孵化(当思考主体不在有意识地思考要完成的创造任务时,潜意识中进行的“思考活动”) 3)启发(一个好点子忽然从脑海中冒出来) 4)验证(具体化这个点子并验证它的有效性)的创造力过程模型。
1967年美国心理学家J. P. Guilford则在论文《人类智能的本质(The Nature of Human Intelligence)》中区分了收敛型思维(Convergent Thinking)和发散型思维(Divergent Thinking),并提出创造力源于发散型思维的说法。关于创造力的理论模型,在这个时期如雨后春笋。
而这个时候,也正是人工智能作为一个新兴领域正式出现在公众视野的早期发展阶段。创造力作为人类智能的一个集中表现,自然也吸引了人工智能研究者的目光。早期的人工智能研究者Newell、Shaw和Simon就在1963的论文《创造性思考的过程(The process of creative thinking)》中提出了将一件作品或者一个问题的解答判定为“创造性”的四个标准:
- 作品或解答是新颖的、有价值的(对创作者或者对整个社会来说)
- 作品或解答呼吁人们打破之前的成见
- 作品或解答是在强大的动力和执念下被创造出来
- 作品或解答是将原本边界模糊的问题或主题进行了更清晰的解读之后的结果。
在众多这些理论中,我们接下去就来介绍其中的两种对创造力机理的解释:概念空间(Conceptual Space)探索理论和概念整合(Conceptual Blending)理论。这两种理论融合了其他理论中的洞见而较有代表性。更重要的是,从计算创意学的角度来说,这两种理论所提供的创造力过程看起来很有被算法化的希望。
这次的文章,我们就先来详细考察概念空间(Conceptual Space)探索的理论。这个理论最初是在认知科学学者玛格丽特·安·博登(Margaret Ann Boden)的著作《创造力心智(The Creative Mind: Myths and mechanisms)》中被正式提出,后来又在AI学者G A. Wiggins的论文《描述、分析和比较创造力系统的框架(A Framework for Description, Analysis and Comparison of Creative Systems)》中,从数学和形式理论的角度得到了更严谨的重构。

概念空间探索的比喻
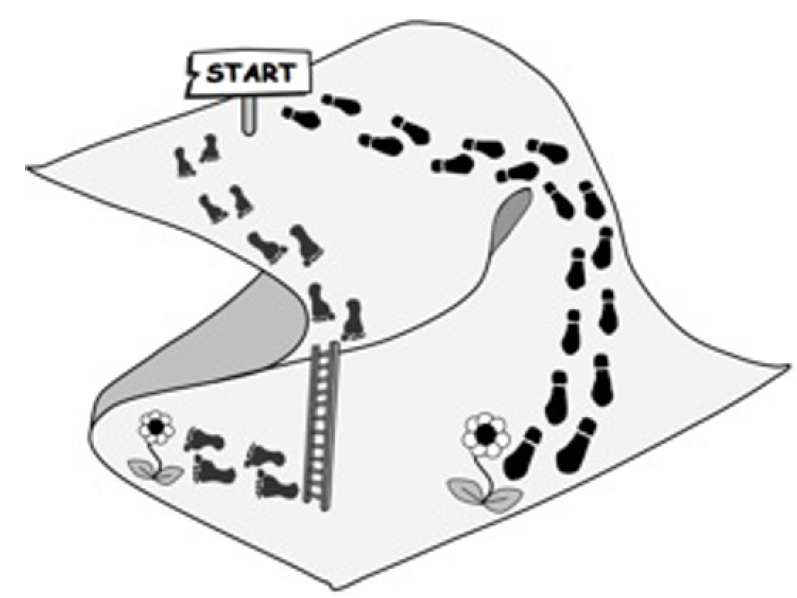
当人们在抽象意义上描述创造力时,常常把所有关于作品的点子所组成的集合比喻成是一个物理意义上的空间。从而创作的过程就可以被比喻为在这个空间中进行探索寻宝,寻找一个符合某种价值判断的作品(的点子)。而那些能够被称得上是“具有创造性”的作品,不仅仅要高度符合价值判断,还必须具有一定的新奇性(Novelty),让人眼前一亮,甚至有思路被颠覆的感觉。
这个空间理所当然应该非常非常地庞大——如果空间很小,一眼就能看清它的每一个角落,就不存在在其中发现什么人们没见过的新奇宝藏的可能。这个空间同时也应该不是一马平川的,而应该是各种山路崎岖错综复杂,有着许多人迹罕至的隐藏地点——这样当人们在那些隐藏地点发现宝藏的时候,才能惊讶于这个常识所熟悉的栖息地竟还有着这样不为人知的世外桃源。
我们将这个空间称之为“概念空间(Conceptual Space)”,因为它实际上是人们脑海中对某一个领域所有可能的作品的概念所组成的抽象的空间。
一种比喻性的说法能够帮助人们理解复杂的概念,但打比方显然不是严谨的科学探讨。因此接下来,我们用更加准确的语言来描述上面这些比喻性的说法。
(本小节接下去的内容会有较多术语的定义,读起来会有些枯燥,但为了能理解到后面小节讨论的有趣之处,希望大家这里坚持一下 ^_^)
首先,我们有一个被探索的空间,这个空间在数学意义上是某个领域的一切可能被想到的点子的集合,既包括那些司空见惯的平庸的点子,也包括任何灵光一现得到的奇思妙想,甚至包括那些语无伦次的、根本毫无意义的点子——哪怕是一个什么内容都没有的空白点子,我们也将它看作是一个特殊的点子包括在这个空间中。我们将这个空间称作全域(Universe)。
显然,全域中包含了大量毫无意义的点子。一个点子没有意义的方式可能有很多:可能这个点子本身就站不住脚,不能自洽;可能这个点子虽然逻辑上没有问题,但它无法被具现化成为一个作品;也可能这个点子无法导向任何符合当前创作主题的作品。
为了排除掉这些毫无意义的点子,我们假设对应某个创作主题存在一套定义规则,将那些有意义的点子区分出来。定义规则的数学本质是一个将集合映射到它的子集的函数:将任意一个点子集合代入这个函数的自变量,就得到这个点子集合中有意义的那部分点子组成的子集。
因此,将全域作为自变量代入定义规则函数,就得到一切有意义的点子组成的集合,我们将这个集合称作是概念空间(Conceptual Space)。
有读者可能会质疑,一个点子是不是有意义,真的是非黑即白的事情吗?尤其在艺术创作的领域,一件作品是不是符合创作主题,答案可能是模棱两可的。为了回应这个质疑,我们可以适当泛化(Generalize)我们这里所使用的集合概念,使用模糊理论(Fuzzy Theory)中的模糊集合(Fuzzy Set)的集合定义。
模糊集合是一种边界模糊的集合。在传统的集合中,一个数学实体是不是一个集合的元素,这个问题的答案只有是或不是两种,因此集合有很明确的边界。而一个数学实体是不是一个模糊集合的元素,这个问题的答案是0和1之间的某个实数——答案越接近1,这个数学实体就越属于这个模糊集合——因此模糊集合的边界可以是一个模棱两可的灰度地带。
因此,概念空间就可以被看作是有意义的点子所组成的一个模糊集合。
为了将概念空间探索这个非科学性的比喻转化为科学性的理论,我们还需要去定义这个语境下“探索”这个概念的含义。“探索”意味着,在某个空间中,以某种顺序去“考察”这个空间中的实体,将未知的实体转变为已知的实体——扩大已知实体所组成的子空间——并在这个过程中掌握某个搜索目标相关属性在这个空间中的分布。
这里的关键是,“按某种顺序”去查阅。正是这种查阅顺序在荒蛮无序的概念空间中开辟了道路、建立了方位感,也为探讨“某个搜索目标相关属性在这个空间中的分布”提供了基础。
于是,我们在概念空间探索的理论中再引入遍历(Traversal)规则这个概念。遍历规则告诉一个思考主体,从某一个作为起点的点子出发,如何到达下一个需要去考察的点子,以此赋予这个思考主体在概念空间中四处移动探索的能力。
遍历规则的概念,对应到人作为创造力的主体的情况,来源于每个人不同的思考、联想习惯和在这个领域积累的经验和技能等等,因此理所当然是因人而异的。从梵高的《星空(The Starry Night)》出发,有的人会考虑这种冷彻之下暗藏熊熊燃烧的热忱的情绪还能以什么其他的方式进行表达,有的人则会着眼于鲜亮的蓝色和黄色的对比而思考这种色彩运用还能出现在什么其他的情境下。
一个领域的高手和初学者也自然会有不同的遍历规则——一个极有经验的大师会快速跳转到他擅长的子空间、或者本能性地知晓某个子空间是不会有结果的,而初学者则可能有更加保守谨慎的探索作风、也更容易误入歧途。
当然,考察点子的顺序也不完全由创造力主体自身的探索能力和探索习惯决定,它还跟规定了当前探索目标的定义规则相关。在不同的创作主题面前,创作者很自然会改变点子的考察顺序。
另一个对考察点子的顺序造成影响的因素是创作者的审美倾向。设想一个创作者由一个点子出发,想到了多个点子可以作为下一个考察对象,这个时候,主体的审美倾向——或者说主体对点子潜在价值的判断,就决定了选择其中哪一个点子进行考察。
因此,我们再引入价值函数的概念。价值函数是将全域中的元素映射到实数的函数——将任意一个点子作为自变量代入价值函数,就得到一个反映了这个点子可能带来的审美价值的量化数值。
因此,代表创作者自身能力和思考联想习惯的遍历规则、规定了创作主题的定义规则和代表创作者的审美倾向的价值函数,共同决定了在概念空间中进行探索的顺序。
将遍历规则、定义规则和价值函数放在一起组成一个三元组,这个三元组构成了一个将全域中的元素映射到全域中的元素的函数——将一个点子作为自变量代入这个三元组构成的函数,就得到另一个点子,作为创作者下一个考察的目标。
读者可能注意到,这个三元组的子变量和因变量都是全域中的点子,而不是概念空间中的点子。这是为了描述一个创造力主体的探索误入歧途的情况——三元组返回了一个非概念空间中的点子,也就是一个无意义的点子,作为下一个考察目标。
对于有的创作者来说,这个时候探索就陷入了僵局。而对于另一些创作者来说,这个时候探索还能进行下去,不断将得到的无意义点子代入三元组函数,最终神奇地回到概念空间,并出现在一个意想不到的地方,得到情理之中意料之外的结果。
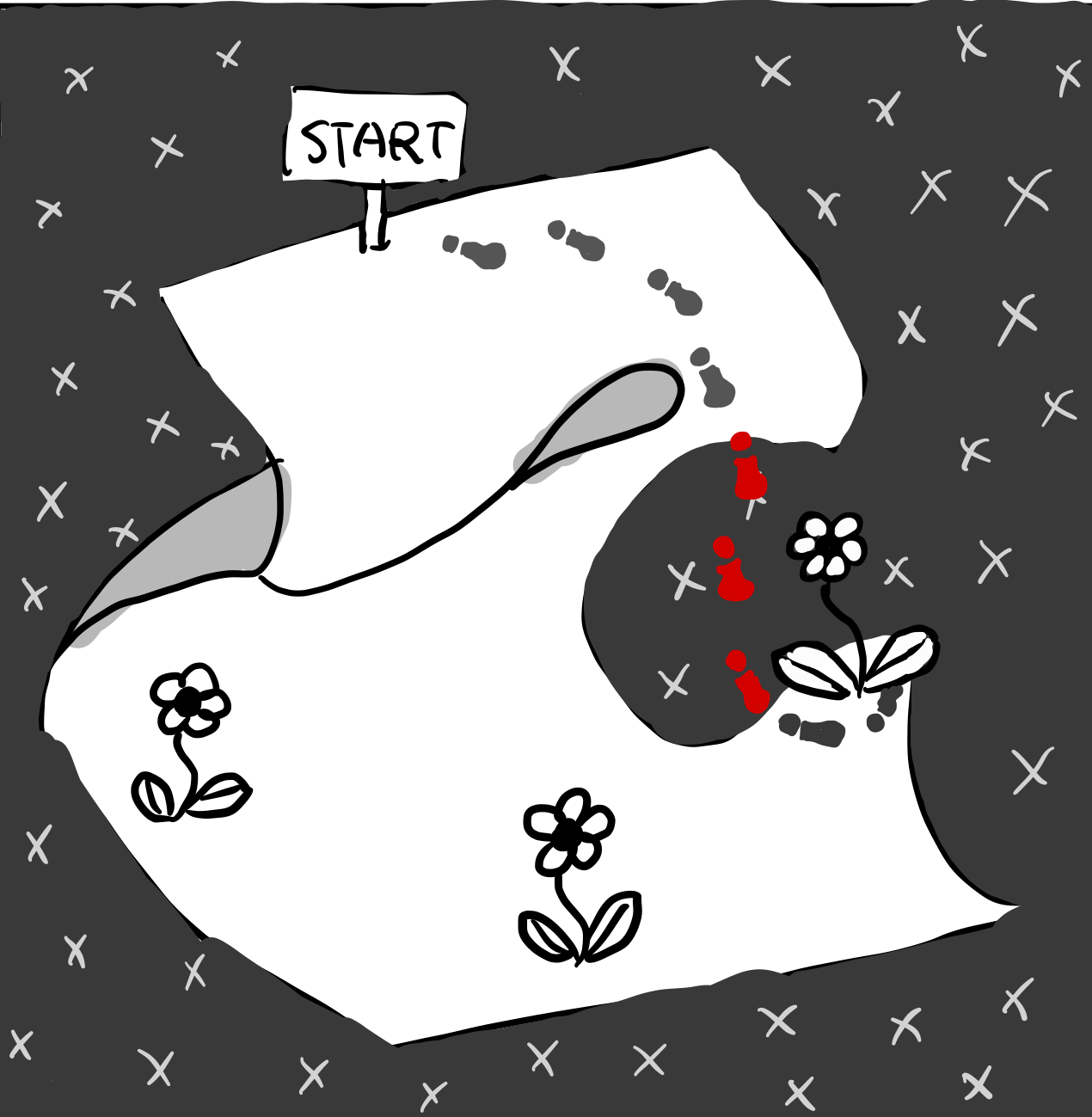
另一方面,既然遍历规则是与具体的某个创作者挂钩的,受限于这个创作者的思考联想能力和技能经验,完全有可能概念空间中的某些点子在一个特定的三元组函数下无论也不可能得到——对应于这个创作者在当前创作上下文下无论如何也想不到的点子。也就是说,一个特定的三元组函数,不需要能够穷尽概念空间中的所有元素。
前面提到,我们将没有任何内容的点子也作为一个点子的特例包括在全域之中。而将这个没有任何内容的空白点子作为自变量代入三元组函数,我们就得到了一个创作者在面对一个创作主题时会首先去考察的点子。
至此,我们定义了全域,定义规则,概念空间,遍历规则,价值函数这五个基本概念。在此基础上,接下去我们就来定义创造力的概念。
探索性创造力(Exploratory Creativity)和转型性创造力(Transformational Creativity)
根据概念空间探索的比喻,一种对创造行为的简单理解是:
某个创作者,通过在概念空间中进行探索,得到了一个极具价值的之前从未被发现的点子。
或者用前面一部分定义的各种术语,可以这么表达:
创作者运用某个遍历规则在概念空间中进行探索,得到了一个在价值函数中代入后取值非常高的新点子。
听起来似乎合理,不过,这个定义好像遗漏了什么。
确实,发现了一个未被发现过的极具价值的新点子是创造力的一种表现。但是,那些历史上真正颠覆世人眼界的惊世天才的创作,似乎还不仅仅于此。
他们的贡献不仅仅在于过去未被发现过的极具价值的点子。更重要的是,他们的点子往往还颠覆了人们对某个领域的固有认知,提示人们用一种彻底不同的视角去看待这个领域。
比如说,非欧几何的发明,意义不仅仅在于它在广义相对论中的应用价值,还在于它颠覆了人们对于欧氏几何中平行公设必须成立的成见。
虚数的发明,意义不仅仅在于它在傅里叶变换和量子力学等的应用价值,还在于它颠覆了人们“负数开平方没有意义”的成见。
抽象派艺术风格之所以能够一度成为风潮,光靠作品的审美价值是不够的,更重要的原因还是它对人们“美术需要摹仿自然”的成见的打破。
2007年首次发布的iPhone之所以能引起手机市场彻底革新,也不仅仅是因为iPhone手机本身好用,还因为iPhone系列手机打破了当时“手机只是打电话发短信的工具”的成见,为整个手机市场打开了新世界的大门。
等等等等。
这种颠覆性,正是上面的对于创造力的定义所遗漏的。
为了回应这个反论,我们将上面定义的创造行为先称作是“弱创造力”,而承认另外还存在一种“强创造力”,符合上面所说的这种直觉。
在“弱创造力”中,由于不同创作者的区别只在于遍历规则,高价值新点子的发现,往往被归功于遍历规则的有效性。
而在“强创造力”中,高价值新点子的发现不仅仅是应用某个遍历规则的结果创作者往往改变了整个问题的定义,以全新的视角重新定义了这个问题。
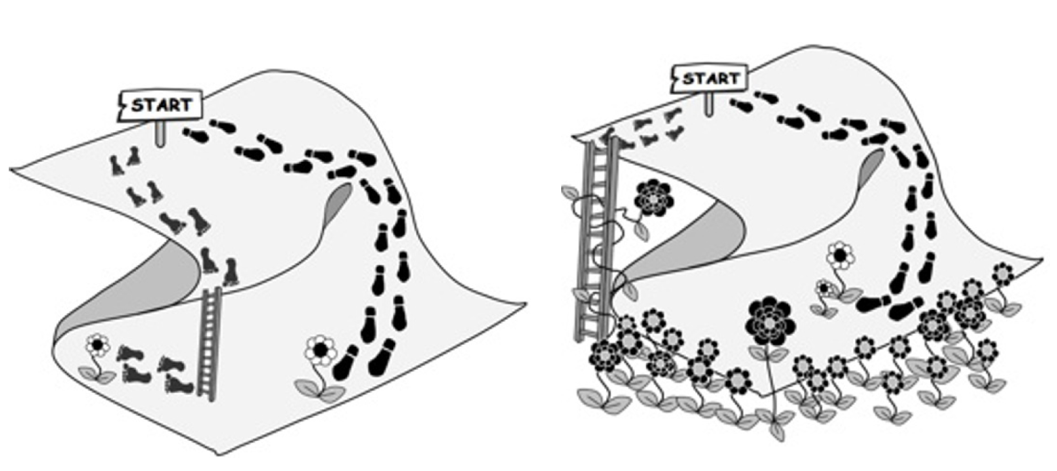
也就是说,“强创造力”的创作者,改变了社会认知中的定义规则。创作者最后发现的高价值新点子过去之所以没有被发现,可能就是因为这个点子在社会认知中的定义规则下不存在于(或过于隐晦地存在于)概念空间中,而只有在使用新的定义规则后才能在概念空间中被发现。
而这个高价值新点子最后会被世人所接受,并成功颠覆世人对这个领域的认知,意味着这个新的定义规则比原来社会认知中的定义规则更加接近真正的定义规则。
“强创造力”是一种与“弱创造力”截然不同的能力吗?
我们进一步思考,“强创造力”的创作者是如何找到新的定义规则的?
“强创造力”的创作者改变了问题本身:从如何找到一个高价值的新点子的问题出发,他们转而关注一个新的问题——如何找到一个更容易找到高价值新点子的概念空间——由于概念空间是由定义规则决定,这个问题实际上是如何找到一个更容易带来高价值新点子的定义规则。
如何找到这个新的定义规则?创作者需要在另一个包含了所有可能的定义规则的概念空间中进行探索,为此需要一个定义规则的定义规则,一个判断定义规则在多大程度上能带来高价值新点子的价值函数,以及在这个全新的概念空间进行探索的定义规则的遍历规则,最终找到一个高价值的定义规则。
于是,我们可以这样定义这种“强创造力”:
创作者在定义规则的概念空间进行探索,得到了一个比当前社会公认的定义规则更接近真正的定义规则的定义规则,在新的定义规则下进行探索得到了一个极具价值的未被发现的新点子。其结果不仅仅是新点子,还有新的定义规则。
我们发现,“强创造力”的本质,是在定义规则的概念空间——一个高阶(Meta)概念空间中的“弱创造力”。“强创造力”与“弱创造力”的创作者真正的差别,就在于构造这种高阶概念空间的能力。而一旦高阶概念空间被构造出来,创作者在其中进行的仍然是类似于在“低阶”概念空间中进行的探索。
我们这里所说的“弱创造力”,由于单纯的是在一个给定概念空间中进行探索的结果,在学术界的正式名称是"探索性创造力(Exploratory Creativity)"(由认知科学学者玛格丽特·安·博登命名);相应地,“强创造力”因为是将给定概念空间进行了转型之后的结果,它的正式名称是“转型性创造力(Transformational Creativity)”。
高阶概念空间:从内容到形式的跳跃
高阶概念空间是一个什么样的空间?与原来的“低阶”概念空间有根本性的差别吗?
“低阶”概念空间是某个领域所有可能的“点子”所组成的全域的一个子集。相应地,高阶概念空间就应当是所有可能的有关定义规则的点子所组成的“定义规则的全域”。
前面提到,定义规则的数学本质是一个将点子的全域映射到它的子集的函数。那么定义规则的全域,就应该是所有这样的函数所组成的集合。
如果我们为每一个点子分配一个独一无二的符号序列,用这个符号序列来代表这个点子。那么,点子的全域就可以被看作是代表点子的所有符号序列所组成的集合,而概念空间则是这个集合的子集。
在数学和计算理论中,将一个符号序列的集合映射到这个集合的子集的函数,可以用一种叫做形式语言(Formal Language)的数学对象来表示。
形式语言是一种抽象意义上的语言——它只有语法,没有语义。一个形式语言是一系列与语义无关的语法规则,规定了一个任意的符号序列什么时候是这个语言的符合语法的句子。
通过给出语法规则、定义这样的形式语言,我们能够将一个符号序列的集合区分为符合语法规则的子集和不符合语法规则的子集。因此,一个形式语言也可以被看作是一个将符号序列的集合映射到它自身的子集的函数,与我们前面讨论的定义规则就具有了相同的数学本质。
而如果我们用一套形式语言来表示一个定义规则,那么定义规则的全域就是所有这样的形式语言的集合。而由于所有这个形式语言的符号表都已经被用以编码点子的那些符号所限制,定义规则的全域就是符号表为这些符号的所有语法规则的集合。
当转型性创造力主体进行创作时,它就是在这样一个高阶概念空间探索。
有趣的是,低阶概念空间由于是由当前创作领域中所有可能的点子组成,它的内容是与当前创作领域息息相关的——空间中的每一个点子都是在述说有关创作领域下的某个“内容"。而高阶概念空间中的元素是完全抽象的语法规则,它们已经跟当前的创作领域没有任何内容上的联系了。
不论低阶概念空间是关于哪个创作领域的,在进行转型性创作力行为时所构造的高阶概念空间,实际上都是一样的。
这也意味着,尽管探索性创造力产生一个新点子的机理,可能视创作领域的不同而有所不同,但不同领域的转型性创造力的运作方式却更有共通之处。
如果我们更进一步去讨论“高高阶(meta of meta)”概念空间,或者说定义规则的定义规则的定义规则,我们发现:高阶概念空间的元素--语法规则,本身仍然可以用符号序列来编码(即给每一个不同的语法规则分配一个独一无二的符号序列)。
而“高高阶”概念空间的元素,不过是编码语法规则所使用的符号下的语法规则。因此“高高阶”概念空间的数学本质与高阶概念空间并无不同。只要能够做到在“第一阶”的高阶概念空间中搜索,就能够在“任意阶”的高阶概念空间中搜索。
也就是说,即使是在一个高阶概念空间中进行转型性创造力行为,所构造的'“高高阶”概念空间,还是与任意低阶概念空间下构造的高阶概念空间,并无实质性不同。
因为,不论是高阶概念空间还是“高高阶”概念空间,其成员都是脱离了语义的单纯的语法规则。
而这正是由于高阶概念空间的内容无关性。通过转向高阶概念空间,创作者实现了从内容向形式的跳跃。
后语
这一章中,我们考察了源于概念空间探索这个比喻的创造力理论框架,定义了概念空间的概念,根据创作者是否改变了给定的概念空间,将创造力区分为探索性创造力和转型性创造力。我们发现,转型性创造力的本质是高阶概念空间的探索性创造力。
我们进一步探讨了高阶概念空间的本质,发现它实际上是一个脱离语义的语法规则组成的集合。通过构造高阶概念空间,创作者实现了从内容向形式的跳跃。
我个人认为,这种跳脱内容关注形式的能力,也正是一个创作者能够在多大程度进行转型性创造的核心所在。
而计算机作为一种符号机器,它所擅长的正是形式层面的操作,反而不像人类那样倾向于被内容所限制了思考。
比如说,来自八竿子打不着的两个毫无关联的话题的概念,人类会因为缺乏它们同时出现的经验而很难将它们联系起来。而对于根本就没有任何经验的计算机来说,只要观察到这两个概念编码上的相似之处,就能毫无违和感地在它们之间建立关系。
从这个角度来看,将创造力进行算法化,似乎是很有希望的。
但另一方面,高阶概念空间中搜索到的概念,还是要重新落地到低阶概念空间,其价值才能得到评估。
擅长形式层面的操作而不擅长内容形式层面的操作的计算机,因此就不擅长这种落地和评估。即使它在高阶概念空间发现了大量有潜在价值的点子,无法在内容层面上说服它的人类用户相信这些点子的价值,甚至是不是可以认为它自己对这些点子的价值有所认知都是个问题。
这样的创作过程,也很难被称为是一个创造力行为。
这可能才是制造出人工创造力真正的难点所在。
我们今天介绍了一个理论框架,来为今后的讨论打下基础。但今天的讨论还只限于问题的表层——我们只解释了“创造力是一种什么现象”的问题,而并没有进一步探讨是什么引起了这个现象。
高阶概念空间中的探索是怎样的?高阶概念空间中的发现如何被落地成为低阶概念空间的新点子?作为创作者的一种能力的创造力,究竟是一种什么样的能力?
下一章我们就来介绍另一套理论:概念整合(Conceptual Blending)理论。看看它如何回答上面的这些问题。
参考文献
Wikipedia "Creativity"
Wikipedia "Computational Creativity"
Wikipedia "Formal Language"
Wiggins G.A. (2019) A Framework for Description, Analysis and Comparison of Creative Systems. In: Veale T., Cardoso F. (eds) Computational Creativity. Computational Synthesis and Creative Systems..
Boden, M. A. (2004). The creative mind: Myths and mechanisms (2nd). London:Routledge.
Newell, A., Shaw, J., & Simon, H. (1963). The process of creative thinking. In G. T. H. E. Gruber & M. Wertheimer (Eds.), Contemporary approaches to creative thinking. New York: Atherton.
Wallas G. (1926). The Art Of Thought. New York, NY: Harcourt Brace
Guilford, J. P. (1967). The Nature of Human Intelligence.
Veale, T. (2012). Exploding the creativity myth: The computational foundations of linguistic creativity. London, UK: Bloomsbury.
附录:一个形式语言的例子

这个形式语言由0,1两种符号组成。
它的语法规则规定:
1)"01"是一个合法符号序列;
2) 在任意一个合法符号序列左边加一个"0"右边加一个"1",得到的还是一个合法符号序列
根据这个语法规则,"01"和"000111"是合法符号序列,而"001111","000101" 和 "a000b111"不是合法符号序列
可以发现,任何一个含有相同数量的"0"和“1”符号且不含其它符号的符号序列,只要所有的“0”都在左边所有的“1”都在右边,它就是这个形式语言的一个合法的句子。反过来,任何一个合法的句子都含有相同数量的"0"和“1”符号且不含其它符号,并且所有的“0”都在左边所有的“1”都在右边。
形式语言只规定了语法,对符号序列的含义没有任何定义。